ООО Архитектурная Производственная Компания

ОПРЕДЕЛЕНИЕ РАСЧЁТНЫМИ МЕТОДАМИ ПРЕДЕЛОВ ОГНЕСТОЙКОСТИ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

В.В. Жуков, И.С. Молчадский, В.Н. Лавров

Статья опубликована в издании «Бетон и железобетон – пути развития. Научные труды 2-ой Всероссийской (Международной) крнференции по бетону и железобетону. 5-9 сентября 2005 г. Москва; В 5 томах. НИИЖБ 2005, Том 2. Секционные доклады. Секция «Железобетонные конструкции зданий и сооружений»., 2005.»

Минимальные пределы огнестойкости строительных конструкций можно опреде-лять согласно СНиП 21-01-97* не только их испытанием, но и расчётом. Последнее, как правило, целесообразно использовать для большепролётных статически неопределимых конструкций. Но при этом необходимо соблюдать некоторые правила, связанные с физи-кой процесса и применением существующих расчётных программ. Физика процесса при расчёте железобетонных конструкций при высокотемпера-турном относительно кратковременном воздействии должна отвечать следующим требо-ваниям:

Учитывать тепловое воздействие при развитии температуры при пожаре по стандарт-ной кривой температура-время. Это позволяет сравнить правильность расчёта при оп-ределении распределения температуры в конструкции с её распределением в экспери-ментальных исследованиях.

Учесть фазовый переход воды в пар в структуре бетона. Фактически фазовый переход происходит в “среднем” бетоне класса В20-В50 при температурах 100-2000С. Принятая температура фазового перехода 450С [1] является условной и не отвечает физике про-цесса. Классически учёт фазового перехода при расчёте температуры в железобетонной конструкции при пожаре следует выполнять по методике решения задачи Стефана - методом сглаженных коэффициентов [2]. И не смотря на этот достаточно физически точный метод, следует иметь в виду, что он так же является несколько условным, так как в целом наблюдается сложный процесс тепло- и массопереноса [3]. В любом случае расчёт нужно сравнить с экспериментальными данными, что и сделано при применении метода энталь-пии (замене в уравнении Фурье С-удельной массовой теплоёмкости, на объёмную с*y, где y- средняя плотность бетона) [4]. Можно так же использовать уравнение Фурье с дополни-тельным членом, учитывающим затраты тепла на фазовый переход воды в структуру бетона.

В термомеханическом процессе при его расчёте необходимо учесть неупругие дефор-мации бетона, главным образом его ползучесть при высокой температуре, так, как бу-дет показано далее, относительные деформации ползучести при действии высокой температуры и нагрузки будут значительно больше относительных силовых деформа-ций [5]. Прежде чем считать усилия, напряжения и деформации в сложных конструкциях необходимо их сравнить с имеющимися в достаточно большом количестве эксперимен-тальными данными для более простых [5, 6] и только после этого использовать расчётную программу, например, Stark, Cosmos и др. По нашему мнению, для оценки несущей способности статически не определимых железобетонных конструкций при пожаре целесообразно использовать метод предельного равновесия [7]. Для этого нужно иметь соответствующий инженерный опыт расчёта, дан-ные о схеме разрушения конструкции, желательно при тепловом воздействии, при пожаре и внешней нагрузке. Следует иметь в виду, что при использовании компьютерной техники желательно принимать теплофизические и физико-механические свойства бетона и арматуры по меж-дународным экспериментальным данным [6] с учётом отечественных результатов исследований [1,8]. При этом нужно внимательно отнестись к составу бетона и классу арматуры, так как от них зависят их свойства при высокой температуре [9,10]. Большое влияние на результаты расчёта оказывают начальные и граничные условия. Поэтому не точный выбор расчётной схемы может привести к значительным погрешностям. Приведём пример методики расчета, который часто используется в европейских работах [5]. Примем, что общие относительные деформации бетона E1 при нагреве в загруженном со-стоянии состоят из:

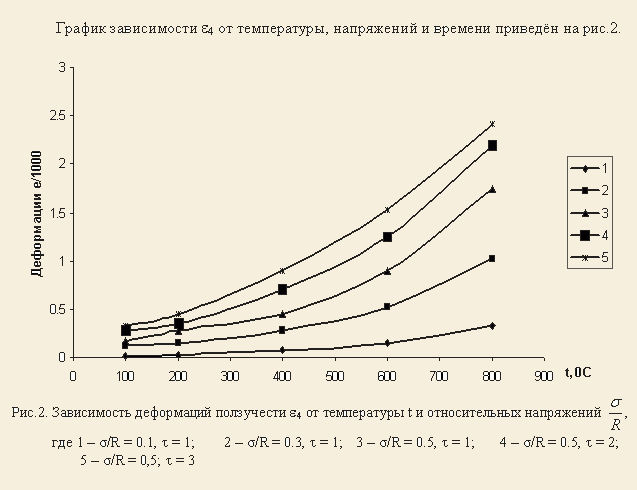
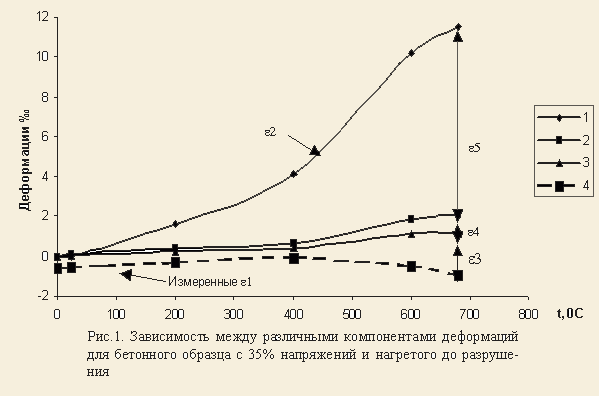Анализ зависимости деформации от напряжений, температуры и времени показал, что теоретически наиболее сложно описать деформации ползучести при постоянной температуре и постоянном напряжении сжатия. Эти деформации можно при данном виде загружения принять в виде [5]:

Деформации ползучести Е5, развивающиеся под напряжением при увеличении тем-пературы практически не могут быть измерены и определяются как разница между замеренными общими деформациями Е1 и другими тремя компонентами

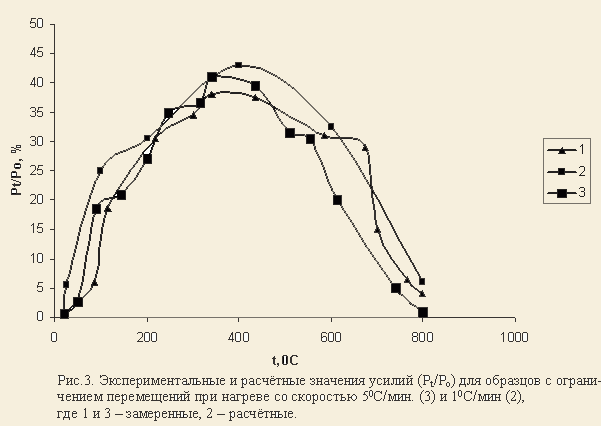
С использованием равенства (1) выполним расчёт сжимающих усилий (Pt) в бетон-ной призме при равномерном нагреве по её сечению и длине, имеющей ограничения пе-ремещений по торцам по оси Х (рис. 3). Относительные усилия Pt/P0 определим по формуле:

Результаты расчёта и экспериментальные значения Pt/P0 приведены на рисунке 3. Видно, достаточно удовлетворительное совпадение (для цели оценки усилий при расчёте на огнестойкость) теоретических и опытных значений усилий и, главное, соответствие из-менению усилий при нагреве. Следует отметить, что усилия, по крайней мере, в диапазоне (1-5)С/мин. как правило, не превосходят значений 0,5Pt/P0. Последнее несколько упрощает расчёт.

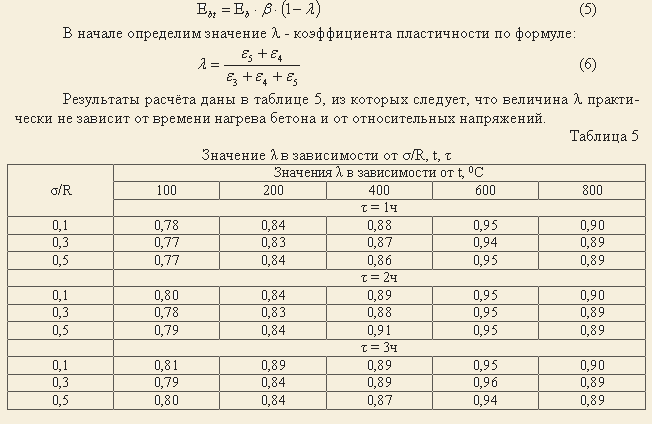
Рассмотрим расчёт более сложной конструкции – железобетонной статически неопределимой балки. Для этой цели используем модуль деформации [12]:

На основании изложенных физических процессов деформаций в статически неопредели-мых железобетонных конструкциях. Приведём сравнение результатов расчёта с экспери-ментальными данными. Из этого сравнения видно, что получено хорошее совпадение теоретических значений с опытными, например, момента (рис.4). Анализируя эти данные можно сделать вывод, что наибольшее значение усилий достигается через 1-2 часа тепло-вого воздействия при пожаре, далее во времени моменты уменьшаются.

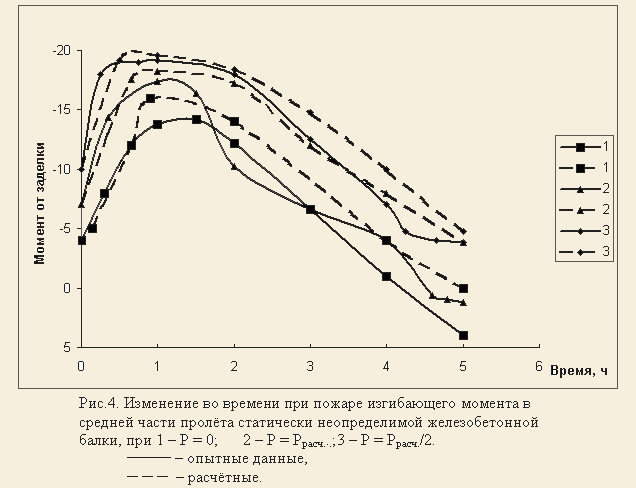
ВЫВОДЫ

При определении расчётного минимального предела огнестойкости целесообразно ис-пользовать модель с деформированием бетона в виде равенства (1). Использование другой модели вызывает необходимость её сравнения с опытными данными.
Для оценки процесса деформирования бетона при тепловом воздействии при пожаре можно использовать метод определения деформаций под нагрузкой [12], широко применяемый при исследовании жаростойких бетонов и огнеупоров.
Для теоретической оценки деформаций ползучести бетона при высоких температурах во время пожара можно использовать выражения (2) и (4). При этом следует иметь в виду, что деформации ползучести, измеренные при постоянных стационарной темпе-ратуре и напряжении, в значительной степени зависят как от относительных напряже-ний (6/R), так и от температуры (t). Неустановившиеся деформации ползучести, учи-тывающие влияние увеличения температуры и действие напряжений от нагрузки, так-же зависят от 6/R и t.
Скорость нагрева бетона в диапазоне (5-1)С/мин. не оказывает влияние на величину температурных усилий.
Температурные усилия (Pt) в конструкциях при нагреве в условиях пожара увеличива-ются при нагреве бетона до 300-400 С и при более высокой температуре начинают уменьшаться, при этом не достигая максимальных значений более 0,5 Pt/P0.
Коэффициент пластичности бетона при нагреве практически не зависит от времени и относительных напряжений.
Температурные усилия в статически неопределимых железобетонных конструкциях во время пожара имеют максимальные значения через 1-2 часа от начала пожара. B дальнейшем они уменьшаются.
Учитывая сложность физических процессов, которые происходят в железобетоне при нагреве, при расчете минимальных пределов огнестойкости следует при определении температурных полей в конструкциях теоретические значения температур сравнивать с их опытными величинами, а для усилий и деформаций теоретические значения срав-нивать с их относительными величинами на простых опытных моделях, прежде чем перейти к расчёту статически неопределимых конструкций. При этих условиях можно использовать предлагаемые модели и расчётные программы для статически неопределимых железобетонных конструкций.

Литература

Инструкция по расчёту фактических пределов огнестойкости железобетонных строи-тельных конструкций на основе применения ЭВМ ВНИИПО, 1975.
Будак Б.М., Соловьёва Е.Н., Успенский А.Б. Разностный метод со сглаживанием ко-эффициентов для решения задачи Стефана. Вычислительная математика и математи-ческая физика. Том 5, № 5, 1965.
Ройтман В.М., Зырина Г.Н. Решение теплотехнической задачи огнестойкости конст-рукций с учётом процессов влагопереноса на ЭВМ по неявной конечноразностной схеме. Огнестойкость строительных конструкций ВНИИПО, 1974.
Kai Oden Fire resistance of prestressed concrete double T – units/ Civil Engineering and building construction, series № 48/ Stockholm, 1968.
Yngre Anderberg – Sven Erik Magnusson – Ove Petterson – Sven Thelanderson – Uld Wickstrom. Analytical design of fire exposed concrete structures. AC I Publication SP – 55, Detroit, 1978.
Properties of materials at high temperatures. Concrete. Kassel: Gesamthochschul – Bibliotek, 1985.
Руководство по расчёту статически неопределимых железобетонных конструкций. Стройиздат, 1975.
Рекомендации по расчёту пределов огнестойкости бетонных и железобетонных конст-рукций. Стройиздат, 1986.
Жуков В.В. Стойкость бетона при действии повышенных и высоких температур.
Милованов А.Ф. Огнестойкость железобетонных конструкций. Стройиздат, 1986.
Мурашев В.И. Трещиноустойчивость, жесткость и прочность железобетона. Машст-ройиздат, 1950.
ГОСТ 23283-78. Метод определения деформаций под нагрузкой при высоких темпера-турах.